Introduction & Crypto basics
보안 코너스톤(Security Cornerstones)
기밀성(Confidentiality)
- 정보에 대한 허가받지 못한(unauthorized) 접근(읽기)를 방지하는 것
무결성(Integrity)
- 정보에 대한 허가받지 못한 쓰기를 방지하는 것
가용성(Availability)
- 사용자가 원할 때 정보에 대한 접근을 제공하는 것
Beyond CIA
- 인증(Authentication)
- 통신 주체가 권리가 있는 사용자임을 보장한다
- standard-alone 시스템의 인증
- 암호화(Cryptography) 기반
- 네트워크 상에서 인증
- 암호화(Cryptography)와 보안 프로토콜 기반
- 인가, 허가(Authorization)
- 인증된 사용자의 행동에 대한 제약사항 적용
- 액세스 컨트롤(access control)
- 인증된 사용자의 행동에 대한 제약사항 적용
- 상기 보안 메커니즘이 소프트웨어에서 구현되었다
- 버그, 바이러스, 웜, 운영체제 보안
보안 위협(Security Threats)
- 위험 원인
- 사람의 실수: 55%
- 불만족스러운(disgruntled) 직원: 10%
- 정직하지 않은(dishonest) 직원: 10%
- 외부 액세스(outsider access): 10%
- 자연재해
- 사람이 대부분을 차지한다
Crypto
- 암호 작성술, 암호학(Cryptology)
- 암호화된 정보를 보호하거나 그것을 원상 복귀시키는 암호 해독법을 포함하는 과학의 한 분야이다.
- 암호화(Cryptography)
- 암호를 만드는 것
- 암호 해독(Cryptanalysis)
- 암호를 해독하는 것
- 암호(Crypto)
- 위 전부를 포함 + 알파
- 암호 시스템(cryptosystem)에서 암호(cipher)는 평문(plaintext)을 암호화(encrypt)하는데 쓰이고, 결과는 암호문(ciphertext)이다 이를 복호화(decrypt)하면 평문이 된다
- 키(key)는 암호화 시스템을 설정하는데 쓰는데, 대칭키(symmetric key) 암호화 시스템은 암호화와 복호화에 같은 키를 쓰고, 공개키(public key) 암호화 시스템은 암호화 할 때 공개 키(public key)를, 복호화 할 때 개인 키(private key)를 사용한다
- 기본적인 가정
- 시스템이 공격자에게 완전히 알려졌다.
- 오직 키만 비밀이다.
- 키르키호프, 커코프, 커크호프, 커차프스의 법칙(Kerckhoff’s Principle): 암호화 알고리즘은 비밀이 아니다.
- 비밀 알고리즘은 노출됐을 때 취약하고, 항상 비밀로 남지 않으므로, 그 전에 취약점을 찾아야 한다
단순 치환(Simple Substitution)
평문을 3만큼 shift 연산한다.
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
Not-so-Simple-Substitution
평문을 {0에서 25} 만큼 shift 연산한다.
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G |
Even-less-Simple Substitution
각 평문에 랜덤 알파벳을 중복 없이 넣는다.
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J | I | C | A | X | S | E | Y | V | D | K | W | B | Q | T | Z | R | H | F | M | P | N | U | L | G | O |
가능한 키: 26! > 288
초당 240 키를 테스트할 수 있는 경우 평균적으로 4450 millennia 시간이 걸린다.
빈도수 분석(Frequency analysis)
- letter frequency: 빈도수
- 2글자: TH, HE, IN, ER, AN, RE, ED, ON, ES, ST, EN, AT, TO, NT, HA, ND, OU, EA, NG, AS, OR, TI, IS, ET, IT, AR, TE, SE, HI, OF
- 3글자: THE, ING, AND, HER, ERE, ENT, THA, NTH, WAS, ETH, FOR, DTH
안전한 암호
안전한 암호는 short-cut attack이 불가능하고, 공격에 필요한 가장 좋은 방법이 exhaustive key search만큼의 노력을 필요로 해야 한다 = 안전하고 길이가 충분히 긴 키 공간을 가져야 한다
이중 전위 암호(Double Transposition Cipher)
평문을 표의 열과 행을 바꾼 값으로 치환한다.
| col 1 | col 2 | col 3 | |
|---|---|---|---|
| row 1 | a | t | t |
| row 2 | a | c | k |
| row 3 | x | a | t |
| row 4 | x | d | a |
| row 5 | w | n | x |
치환(permutation) (3,5,1,4,2) 와 (1,3,2) 를 적용시킨다.
| col 1 | col 2 | col 3 | |
|---|---|---|---|
| row 3 | x | t | a |
| row 5 | w | x | n |
| row 1 | a | t | t |
| row 4 | x | a | d |
| row 2 | a | k | c |
글자를 치환하지 않는다.
일회용 암호(One-time Pad)
| letter | e | h | j | k | l | r | s | t |
|---|---|---|---|---|---|---|---|---|
| binary | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| h | e | i | l | h | i | t | l | e | r | |
|---|---|---|---|---|---|---|---|---|---|---|
| plaintext | 001 | 000 | 010 | 100 | 001 | 010 | 111 | 100 | 000 | 101 |
| Key | 111 | 101 | 110 | 101 | 111 | 100 | 000 | 101 | 110 | 000 |
| Ciphertext(Plaintext XOR Key) | 110 | 101 | 100 | 001 | 110 | 110 | 111 | 001 | 110 | 101 |
| s | r | l | h | s | s | t | h | s | r |
- 가장 안전한 암호?
- 이중 스파이는 발신자가 암호문에 가짜 키를 사용했다고 주장한다
- 발신자가 캡처되고 키가 다음과 같다고 주장한다
- 111 101 000 011 101 110 001 011 101 101
- 암호문이 평문의 정보를 제공하지 않는다.
- 패드(Pad)는 항상 무작위여야 하고, 한번만 사용되어야 한다
- 공격 방법(두 번 이상 패드가 사용되었을 때)
- C1 = P1 XOR K , C2 = P2 XOR K
- 공격자가 (P1, C1)를 알면
- (C1 XOR C2) XOR P1 = (P1 XOR K XOR P2 XOR K) XOR P1 = P1 XOR P2 XOR P1 = P2
- 이 방법은 실용적이지 않다(impractical)
- 비밀 키를 어떻게 전달해야 하는가?
실제 일회용 암호(Real-world One-time Pad)
- 프로젝트 베노마(Project VENONA)
- 1940년 미국, 소비에트 스파이 핵폭탄에 관한 메세지
- 스파이가 일회용 암호를 미국으로 반입함
- 일회용 암호로 메세지를 암호화
- 일회용 암호문 안의 긴 문자열의 반복 등이 복호화를 가능하게 만들었다.
Codebook
“코드 단어”로 채워진 책
단어 기반의 복잡한 치환 암호
Februar 13605
fest 13732
finanzielle 13850
folgender 13918
Frieden 17142
Friedenschluss 17149
Zimmerman Telegram
- 유명한 코드북
- 미국이 1차세계대전을 승리할 수 있도록 만들었다.
- 영국인이 일부분의 코드북을 복원
Recent History of Crypto
- Claude Shannon(1940’s)
- 정보 이론 과학(science of information theory)의 창시자
- 1949년 논문: 보안 시스템에서의 정보 이론(Information Theory of Secrecy Systems)
- 혼돈(Confusion)
- 평문과 암호문의 상관 관계를 알기 어려워야 한다.
- Ex) Substitution cipher, one-time pad
- 확산(Diffusion)
- 평문을 구성하는 각각의 비트들의 정보가 여러개의 암호문 비트에 영향을 미쳐야 한다.
- Ex) Double transposition cipher
- one-time pad가 안전하다는 것을 증명했다.
- 혼돈(Confusion)
- Computer revolution
- 많은 데이터를 다루어야 함
- Data Encryption Standard(DES) (1970’s)
- Public key cryptography(1970’s)
- Advanced Encryption Standard(AES) (1990’s)
- Modern cryptography(2000’s)
암호의 분류법 (Taxonomy of Cryptography)
- 암호화
- 대칭키(Symmetric key)
- 암호화, 복호화 할 때 똑같은 키
- 종류
- 스트림 암호(Stream ciphers)
- 블록 암호(Block ciphers)
- 공개키(Public key)
- 암호화, 복호화 할 때 키가 다르다.
- 전자 서명(Digital signature)
- 해시 알고리즘(Hash algorithms)
- 대칭키(Symmetric key)
- 공격
- 암호문 단독 공격(Ciphertext only attack)
- 기본적이고 언제나 가능하다.
- 알려진 평문 공격(Known plaintext attack)
- 공격자가 몇몇 (평문, 암호문) 쌍을 안다
- 이메일 헤더같은 진부한 헤더(stereotypical headers)를 사용한다
- 선택 평문 공격(Chosen plaintext attack)
- 평문을 입력하면 암호문을 얻을 수 있는 상황에서 공격한다
- Lunchtime attack
- 사용자가 점심 먹으러 나가는 동안 암호 해독 기능을 가진 사용자의 컴퓨터가 공격자가 이용할 수 있다
- 적응형 선택적 평문공격(Adaptively chosen plaintext attack)
- 공격자가 원하는 평문에 대한 암호문을 얻을 수 있는 상황에서의 공격방법이다. 공격자가 자유롭게 평문을 선택할 수 있고, 선택한 평문에 대한 결과에 따라 다음 평문을 선택한다는 점에서 강력한 공격방법이다
- 암호문 단독 공격(Ciphertext only attack)
대칭키 암호화(Symmetric Key Crypto)
- 스트림 암호(Stream cipher)
- 키가 상대적으로 짧다
- 키가 긴 키 스트림으로 확장된다
- 키 스트림이 일회성 암호(one-time pad)처럼 동작한다
- 과거에는 유명했지만 최근 블록 암호만큼 유명하지 않다(사장되는중)
- Shamir: “the death of stream ciphers”
- 하드웨어 단에서 효율적이다
- 목소리 등을 따라가기 위해 속도가 필요하다
- 오늘날 프로세서는 빠르기 때문에 소프트웨어 기반 암호화는 충분히 빠르다
- 종류
- A5/1
- shift 레지스터 기반
- GSM 휴대폰 시스템에 주로 사용된다
- 암호화 과정
- 3개의 순차적인 피드백 쉬프트 레지스터(LFSR: linear feedback shift registers)로 이루어져 있다
- X: 19 비트 (x0,x1,x2, …,x18)
- Y: 22 비트 (y0,y1,y2, …,y21)
- Z: 23 비트 (z0,z1,z2, …,z22)
- 키 K: 64 비트, 처음에 X, Y, Z 레지스터를 채운다
- 각 스텝 m = maj(x8, y10, z10) = 세 개의 값을 받아 다수결을 통해 2번 등장하는 비트(1 또는 0)를 기준으로 한다
- 만약 x8 = m이면 X는 xor 연산을 진행한 후 Shift-right 연산을 진행한다 아니라면 연산을 진행하지 않는다 연산을 진행했다면 연산 결과인 t값을 0번 비트에 넣는다
- t = x13 xor x16 xor x17 xor x18
- xi = xi−1 for i = 18,17,…,1 and x0 = t
- 만약 y10 = m이면 Y는 xor 연산을 진행한 후 Shift-right 연산을 진행한다 아니라면 연산을 진행하지 않는다 연산을 진행했다면 연산 결과인 t값을 0번 비트에 넣는다
- t = y20 xor y21
- yi = yi−1 for i = 21,20,…,1 and y0 = t
- 만약 z10 = m이면 Z는 xor 연산을 진행한 후 Shift-right 연산을 진행한다 아니라면 연산을 진행하지 않는다 연산을 진행했다면 연산 결과인 t값을 0번 비트에 넣는다
- t = z7 xor z20 xor z21 xor z22
- zi = zi−1 for i = 22,21,…,1 and z0 = t
- 위 과정이 완료된 후 키 스트림 비트는 x18 xor y21 xor z22 를 연산한 값이다
- 키 스트림을 평문과 XOR 연산하면 암호문이 완성된다
- 3개의 순차적인 피드백 쉬프트 레지스터(LFSR: linear feedback shift registers)로 이루어져 있다
- 쉬프트 레지스터 암호화(Shift Register Crypto)
- 하드웨어단에서 효율적이다(비트 단위 키 스트림)
- 과거엔 소프트웨어에서 구현하기 어려웠지만 최근은 연산 속도의 향상으로 쉽다
- 과거엔 유명했지만 지금도 조금 쓰인다
- RC4
- 변경되는 256 바이트 룩업 테이블(Lookup table)에 기반
- 자기수정식 룩업 테이블(self-modifying lookup table)
- 1byte(8bit)의 인덱스 포인터 두개가 존재(i, j)
- 취약점이 발견되었다
- 소프트웨어 단에서 효율적이다(바이트 단위 키 스트림)
- 테이블은 항상 0,1,…,255의 순열(permutation)을 가지고 있다
- 암호화 과정
- 키가 배열을 구성하고, 배열이 키 스트림을 구성하고, 키 스트림이 암호문을 만들어낸다
- 키를 이용해서 순열을 초기화한다
- 키의 길이 N: 0 에서 256 바이트
- 각 단계에서 암호화
- 현재 룩업 테이블의 원소(element)를 섞는다(swap)
- 테이블에서 키 스트림 바이트(key stream byte)를 선택한다
- 키 스트림 바이트를 이용해, 테이블 원소를 스왑하고 바이트를 선택한다
- 키 스트림 바이트가 one-time pad의 역할
- 첫 256 바이트는 버려져야한다 아니면 공격자에게 노출이 되기 때문
- RC4는 SSL을 포함안 많은 앱에 사용되고, 32비트 프로세서가 아닌 8비트 프로세서에 최적화되어있다
- 키가 동일하다면 배열S의 구성이 같아질 것이고, 여기서 도출된 키 스트림 또한 같아질 것이므로 암/복호화가 가능하게된다.
- 변경되는 256 바이트 룩업 테이블(Lookup table)에 기반
- A5/1
/* KSA(Key-Scheduling Algorithm) */
//초기화 과정
for i = 0 to 255
S[i] = i // 순열 (1에서 255)
K[i] = key[i (mod N)] // K[i]는 임시 배열
next i
j = 0
for i = 0 to 255
j = (j + S[i] + K[i]) mod 256
swap(S[i], S[j])
next j
/* PRGA(Pseudo-Random Gerneration Algorithm) */
i = j = 0
while GeneratingOutput:
i = (i + 1) mod 256
j = (j + S[i]) mod 256
swap(S[i], S[j])
t = (S[i] + S[j]) mod 256
keystreamByte = S[t]
output keystreamByte
endwhile
- 블록 암호(Block cipher)
- 블록 암호 키는 코드북을 결정한다
- 각 키는 다른 코드북을 생성한다
- 혼돈(confusion)과 확산(diffusion)을 모두 사용한다
- 평문과 암호문은 고정된 길이의 블록으로 이루어졌다
- 평문이 블록보다 클 경우 고정된 길이로 나눈다
- 라운드 함수(round function)를 각 라운드(round)마다 진행함으로써 암호화한다(다음 라운드 함수의 인자: 키, 현재 라운드의 결과값)
- 보통 소프트웨어 안에 내장되어 있다
피스텔 암호(Feistel Cipher)
- 블록 암호 설계 방법 중 하나
- 치환(substitution)과 순열(permutation 전위(transposition))의 조합
- 암호화
- 평문을 좌 우 절반으로 나눈다
- 평문 = (L0,R0)
- 각 라운드(i=1,2,…,n)마다 다음을 연산한다
- Li= Ri−1
- Ri= Li−1 xor F(Ri−1,Ki)
- F는 라운드 함수, Ki는 서브키(subkey)
- 암호문 = (Ln,Rn)
- 평문을 좌 우 절반으로 나눈다
- 복호화
- 암호문 = (Ln,Rn)
- 각 라운드(i=n,n−1,…,1)마다 다음을 연산한다
- Ri−1 = Li
- Li−1 = Ri xor F(Ri−1,Ki)
- F는 라운드 함수, Ki는 서브키(subkey)
- 평문 = (L0,R0)
- 공식(formula)이 어떠한 함수 F라도 적용가능하지만, 특정 함수만 안전하다
- 만약 F(Ri−1,Ki) = 0일 경우 암호화가 제대로 되지 않는다
DES(Data Encryption Standard)
- 1970년대 IBM 루시퍼 암호를 기반으로 고안되었다
- NBS (now NIST)에 의해 미 정부 표준이 되었다
- DES 개발은 논란이 많았다(controversial)
- 정부 기관 NSA (National Security Agency)가 비밀리에 연루되어있었다
- 설계 과정이 공개되지 않았다
- NSA가 백도어를 심었을 가능성
- 키 길이가 줄어들었다
- 128 비트에서 64 비트로
- 루시퍼 알고리즘을 약간 변경하였다
- DES의 수비학(Numerology)
- DES는 피스텔 암호(Feistel cipher)이다
- 64 비트 블록 길이
- 56 비트 키 길이
- 64비트의 가장 중요한 비트 8개가 폐기되었다
- 16 라운드
- 각 라운드마다 48비트의 키가 사용됨(서브키)
- 각 라운드는 단순하다
- 보안은 S-boxes 에 의존한다
- DES는 피스텔 암호(Feistel cipher)이다
- 전체적인 DES 구조
- DES 확장 순열(Expansion Permutation)
- 입력 32 비트
- 출력 48 비트
- DES S-box
- 8 치환 박스(substitution boxes) 또는 S-boxes
- 각 S-box는 6비트나 4비트로 맵핑된다
- S-box number 1
- DES P-box
- 입력 32 비트
- 출력 32 비트
- DES 서브키(Subkey)
- 56 비트 DES 키 0,1,2,…,55 로 넘버링
- 키 스케쥴
- 각 라운드마다 48비트의 서브키가 생성된다
- Left half key bits (LK) from DES key 49 42 35 28 21 14 7 0 50 43 36 29 22 15 8 1 51 44 37 30 23 16 9 2 52 45 38 31
- Right half key bits (RK) from DES key 55 48 41 34 27 20 13 6 54 47 40 33 26 19 12 5 53 46 39 32 25 18 11 4 24 17 10 3
- 라운드 i=1,2,…,16 에 대해
- LK = (LK circular shift left by ri)
- Let RK = (RK circular shift left by ri)
- Left half of subkey Ki is permutation of LK bits 13 16 10 23 0 4 2 27 14 5 20 9 22 18 11 3 25 7 15 6 26 19 12 1
- Right half of subkey Ki is permutation of RK bits 12 23 2 8 18 26 1 11 22 16 4 19 15 20 10 27 5 24 17 13 21 7 0 3
- Bits 8,17,21,24 of LK omitted each round
- Bits 6,9,14,25 of RK omitted each round
- DES Last Word (Almost)
- An initial perm P before round 1
- Halves are swapped after last round
- To use the same logic for both encryption and decryption
- A final permutation (inverse of P) is applied to (R16,L16) to yield ciphertext
- None of these serve any security purpose
- Security of DES
- Security of DES depends a lot on S-boxes
- Everything else in DES is linear
- Thirty years of intense analysis has revealed no “back door”
- Attacks today use exhaustive key search
- DES 확장 순열(Expansion Permutation)
DES Cracker "Deep Crack" custom microchip
DES Cracker circuit board fitted with Deep Crack chips
블록 암호 표기법(Block Cipher Notation)
- P = 평문 블록
- C = 암호문 블록
- 평문 P를 키 K를 이용해 암호문 C로 암호화
- C = E(P, K)
- 암호문 C를 키 K를 이용해 평문 P로 복호화
- P = D(C, K)
- P = D(E(P, K), K)
- C = E(D(C, K), K)
트리플 DES(Triple DES, 3DES)
- 56 비트 DES 키는 너무 작지만 너무 많이 쓰이고 있다
- 112 비트 키(K1, K2)를 사용한다
- C = E(D(E(P,K1),K2),K1)
- P = D(E(D(C,K1),K2),K1)
- 키를 두 개 쓰는 이유
- E(D(E(P,K),K),K) = E(P,K)
- 같은 키를 쓰면 결국 한 번 암호화한 것과 같게 된다
- E(D(E(P,K1),K2,K3)
- 키를 세 개 쓰면 너무 복잡하고, 사용하기 어렵게 된다(하위호환성을 고려)
- 보안성은 112 비트면 충분하다
- E(D(E(P,K),K),K) = E(P,K)
- 두 번 암호화하지 않는 이유: C = E(E(P,K),K)
- 여전히 보안성이 떨어진다
- 2DES가 불가한 이유: 약간 실용적으로 알려진 일반 텍스트 공격, rendezvous (meet-in-the-middle attack)
- C = DES ( K1, DES ( K2, P ) )
- For each possible K’i (where 0 < i < 256)
- Compute C’i = DES ( K’i , P )
- Store: [ K’i, C’i ] in table T (sorted by C’i)
- For each possible K”i (where 0 < i < 256)
- Compute C”i = DES-1 ( K”i , C )
- For each possible K’i (where 0 < i < 256)
- Lookup C”i in T not expensive!
- If lookup succeeds, output: K1=K’i, K2=K”i
- C = DES ( K1, DES ( K2, P ) )
DES 역사
- Chronology http://en.wikipedia.org/wiki/Data_Encryption_Standard
- 1973: NBS publishes a first request for a standard encryption algorithm
- 1974: NBS publishes a second request for encryption algorithms
- 1975: DES is published in the Federal Register for comment
- 1976: First and second workshop on DES
- 1976: DES is approved as a standard
- 1977: DES is published as a FIPS standard FIPS PUB 46
- 1983: DES reaffirmed for the first time
- 1986: Videocipher II, a TV satellite scrambling system based upon DES begins use by HBO
- 1988: DES is reaffirmed for the second time as FIPS 46-1, superseding FIPS PUB 46
- 1992: Biham and Shamir publish the first theoretical attack with less complexity than brute force: differential cryptanalysis. However, it requires an unrealistic 247 chosen plaintexts
- 1993: DES is reaffirmed for the third time as FIPS 46-2
- 1994: The first experimental cryptanalysis of DES is performed using linear cryptanalysis (Matsui, 1994)
- 1997: The DESCHALL Project breaks a message encrypted with DES for the first time in public
- 1998: The Electronic Frontier Foundation (EFF)’s DES cracker (Deep Crack) breaks a DES key in 56 hours
- 1999: Together, Deep Crack and distributed.net break a DES key in 22 hours and 15 minutes
- 1999: DES is reaffirmed for for the fourth time as FIPS 46-3, which specifies the preferred use of Triple DES, with single DES permitted only in legacy systems
- 2001: The Advanced Encryption Standard is published in FIPS 197
- 2002: The AES standard becomes effective
- 2004: The withdrawal of FIPS 46-3 (and a couple of related standards) is proposed in the Federal Register
- 2005: NIST withdraws FIPS 46-3
- 2016: GeForce GTX 1080 Ti recovers DES key in 15 days
AES(Advanced Encryption Standard)
- DES를 대체하기 위해 1990년 후기 AES 대회에서 많은 강력한 암호화 알고리즘이 소개되었지만, Rijndael(발음: Rain Doll, Rhine Doll) 알고리즘이 선택되었다
- NSA가 공개적으로 연루되었다
- 투명한 암호화 과정
- DES처럼 반복되는 블록 암호지만 피스텔 암호가 아니다
- 블록 크기: 128 bits
- 종류
- AES-128
- 키 128비트, 10 라운드
- AES-192
- 키 192비트, 12라운드
- AES-256
- 키 256비트, 14라운드
- AES-128
- 라운드 수: 10 에서 14 라운드(키 길이에 비례)
- 치환-순차 네트워크(Substitution-Permutation Network) 기반 서브바이트(SubBytes)
- 바이트 치환(substitution)은 AES의 S-box이다
- 혼돈 개선(Improve confusion)
- 일반 텍스트와 암호 텍스트 간의 관계 확인
- 유일한 비선형(nonlinear) 원소(element)
- Computes multiplicative inverse in GF(28) on irreducible poly. x8+x4+x3+x+1
- Then, bit scrambling:
- In software implementations, usually use a 16*16 lookup table
AES other operations
AES round
AES Implementation
- Efficient software implementation is required
- Straightforward impl is well suited for 8-bit processors (e.g., smart cards), but inefficient on 32-bit or 64-bit processors
- A more sophisticated approach
- Merge all round functions into one lookup table
- Typical SW speeds are more than 1.6Gbit/s on modern 64-bit processors
AES summary
- AES is a modern block cipher supporting 3 key lengths: 128, 192, 256bit
- No attacks have been found better than brute-force
- AES is not based on Feistel cipher
- AES is part of numerous open standards such as IPsec or TLS
- AES is efficient in software and hardware
암호화에서 사용하는 세부적인 알고리즘(각 단계)는 다음과 같다
Add Round Key
Sub Byte
Shift Row
Mix Column
복호화에서 사용하는 세부적인 알고리즘(각 단계)는 다음과 같다
Add Round Key
Inv_Shift Row
Inv_Sub Byte
Inv_Mix Column
IDEA
- James Massey가 고안
- 현대 암호의 거인 중 하나(자주 쓰인다)
- 64 비트 블록, 128 비트 키
- 혼합모드 산술(mixed-mode arithmetic)을 사용한다
- 최초로 서로 다른 수학 연산을 혼합하였다
Blowfish
- Bruce Schneier가 고안
- 64비트 블록, 키는 최대 488비트 변수이다
- 거의 피스텔 암호(Feistel cipher)이다
- Ri = Li−1 xor Ki
- Li = Ri−1 xor F(Li−1 xor Ki)
- 라운드 함수 F가 4개의 S-boxes를 사용한다
- 각 S-box는 8 비트를 32 비트로 맵핑한다
- 키 의존적인 S박스(Key-dependent S-boxes)
- S-boxes가 키에 의해 결정된다
RC6
- Ron Rivest가 고안 (RSA, RC4, MD5를 고안한 사람)
- 변수: 블록 크기, 키 크기, 라운드 횟수
- AES 최종 후보 중 한명이였다
- 데이터 종속 회전(data dependent rotations)을 사용한다
- 알고리즘의 일부로 데이터에 의존하는 것은 이례적이다
TEA(Tiny Encryption Algorithm)
- 거의 피스텔 암호(Feistel cipher)이다
- xor 대신 +와 -를 사용한다
- 구현이 쉽고, 빠르고, 메모리를 적게 사용한다
- 관련 키 공격(related key attack) 가능성이 있다
- eXtended TEA (XTEA)
- related key attack을 제거하지만 조금 복잡하다
- Simplified TEA (STEA)
- 암호화 분석의 예로서 사용되는 안전하지 않은 버전
블록 암호 모델(Block Cipher Modes)
- 여러 블록을 암호화 하는 법
- 각 블록마다 새로운 키를 적용하는 법
- one-time pad만큼 나쁘거나 더 나쁘다
- 각 블록을 독립적으로 암호화 또는 체인(chain) 암호화
- 부분(partial) 블록을 처리하는 방법
연산 모드(Modes of Operation)
- ECB(Electronic Codebook) 모드
- 분명한 일
- 각 블록을 독립적으로 암호화
- 심각한 취약점이 있다
- CBC(Cipher Block Chaining) 모드
- 블록을 서로 연결(chain)시킨다
- 추가적인 요구 없이 ECB보다 안전하다
- CTR(Counter Mode) 모드
- 스트림 암호(stream cipher)와 같이 동작한다
- 랜덤 액세스(random access)로 유명하다
ECB 모드
- Notation: C=E(P,K)
- Given plaintext P1,P2,…,Pm,…
- Obvious way to use a block cipher is
| 암호화 | 복호화 |
|---|---|
| C1 = E(P1, K) | P1 = D(C1, K) |
| C2 = E(P2, K) | P2 = D(C2, K) |
| C3 = E(P3, K), … | P3 = D(C3, K),… |
- 고정된 키 K에 대해 코드북(codebook) 암호의 디지털 버전이다
- 각 키 별로 새로운 코드북
- ECB Cut and Paste 공격
- 평문 “ABCDEFGHIJKLMNOP”를 보낸다고 가정하자
- 64 비트 블록, 8 비트 아스키라고 가정하자
- P1 = “ABCDEFGH”, P2 = “IJKLMNOP”
- 암호문: C1, C2
- 암호문을 중간에 가로채 C1과 C2의 순서를 바꾼다
- 평문은 P2P1로 복호화된다
- “IJKLMNOPABCDEFGH”
- Pi = Pj라 가정하면 Ci = Cj이고 공격자가 Pi = Pj임을 알아채므로, 공격자에게 정보를 주게 된다
- 이미지를 ECB 방식으로 암호화 할 경우 같은 색깔(평문)은 같은 암호문으로 변환되므로 변경된 이미지가 원래 이미지의 실루엣을 보인다
CBC 모드
- 블록은 서로 연결된다(chained)
- 무작위 초기화 벡터(IV: Initialization Vector)가 CBC 모드를 초기화하는데 필요하다
- IV는 무작위이지만 비밀일 필요는 없다
- 암호화
- C1 = E(IV xor P1, K),
- C2 = E(C1 xor P2, K),
- C3 = E(C2 xor P3, K),…
- 복호화
- P1 = IV xor D(C1, K),
- P2 = C1 xor D(C2, K),
- P3 = C2 xor D(C3, K),…
- 동일한(identical) 평문 블록이 서로 다른 암호문 블록을 산출한다
- Cut and paste 공격이 여전히 가능하지만 복잡하다
- 혼동(garbles)을 일으킬 것이다 ???
- 만약 C2가 G로 혼동되면
- P2 != C1 xor D(G, K)
- P3 != G xor D(C3, K)
- 하지만 P4 = C3 xor D(C4, K), …
- 오류에서 자동으로 복구된다
- 이미지를 CBC 방식으로 암호화 할 경우 같은 색깔(평문)은 다른 암호문으로 변환되므로 변경된 이미지가 원래 이미지의 실루엣을 보이지 않는다
CTR(Counter Mode)
- 랜덤 액세스(random access)로 유명하다
- 블록 암호를 스트림 암호처럼 사용가능하다
- 암호화
- C1 = P1 xor E(IV, K),
- C2 = P2 xor E(IV+1, K),
- C3 = P3 xor E(IV+2, K),…
- 복호화
- P1 = C1 xor E(IV, K),
- P2 = C2 xor E(IV+1, K),
- P3 = C3 xor E(IV+2, K),…
데이터 무결성(Data Integrity)
- 허가되지 않은 데이터의 수정을 방지하거자 감지
- 예) 은행 간 자금 이체(Inter-bank fund transfers)
- 기밀성은 좋지만, 무결성은 중요하다
- 암호화를 통해 기밀성 제공
- 무단 폭로(disclosure) 방지
- one-time pad와 ECB 모드 공격에서 보다시피 암호화만으로는 무결성이 보장되지 않는다
MAC(Message Authentication Code)
- 데이터 무결성을 위해 사용된다(기밀성과는 다르다)
- CBC의 잔여물(residue)로 연산된다
- CBC 암호화를 연산하지만, 마지막 암호화 블록만 저장한다
- MAC 연산
- C1 = E(IV xor P1, K),
- C2 = E(C1 xor P2, K),
- C3 = E(C2 xor P3, K),…
- CN = E(CN−1 xor PN, K) = MAC
- MAC은 평문과 같이 전송된다
- 수신자는 받은 평문에 대해 MAC 연산을 진행하여 MAC 값을 비교한다
- 수신자는 키 K를 알아야 한다
- 만약 중간에 1 비트라도 바뀔 경우 MAC 값이 변하기 때문에 오류가 MAC으로 전파(propagates)되어 메세지 중간에 조작이 있음을 알 수 있다
- 기밀성과 무결성
- 한 키로 암호화, 다른 키로 MAC 계산
- 같은 키를 사용하지 않는 이유?
- 마지막 암호화된 블록(MAC)을 두 번 전송하시겠습니까?
- 보안을 추가할 수 없음!
- 다른 키를 사용하여 MAC 암호화 및 계산
- Even if keys are related
- 여전히 암호화에 비해 2배 많은 작업
- 하나의 “암호화”로 기밀성과 무결성 보장이 연구 주제이다
- 대칭키 암호화에 사용
- 기밀성
- 안전하지 않은 채널을 통해 데이터 전송
- 보안이 보장되지 않는 미디어에 안전한 스토리지
- 무결성 (MAC)
- 인증 프로토콜(Authentication protocols)
- 해쉬 함수로 할 수 있는 모든 것
- 기밀성
공개 키 암호화(Public Key Crypto)
- 트랩 도어(trap door) 기반, 일방향 함수(one-way function)
- 한 방향으로는 계산이 쉽지만 다른 방향으로는 어렵다
- 트랩 도어는 키를 생성할 때 쓴다
- 주어진 p와 q에 대해 N=p x q 를 만족하는 N은 계산하기 쉽지만, 주어진 N에 대해 N=p x q 를 만족하는 p, q는 계산하기 어렵다
- 암호화 과정
- 두 개의 키 (공개 키, 비밀(개인) 키)
- 발신인(Sender)은 수신자(recipient)의 공개 키를 사용하여 암호화
- 수신자가 개인 키를 사용하여 암호 해독
- 전자 서명(Digital Signature)
- 개인 키로 암호화해서 서명한다
- 누구나 공개키를 사용해서 검증할 수 있다
- 하지만 개인 키 소유자만이 서명할 수 있다
배낭 문제(Knapsack Problem)
- n 중량의 셋 W0,W1,…,Wn-1과 중량의 합 S가 있다고 하고, 여기서
- S = a0W0+a1W1 +…+ an-1Wn-1를 만족하는 ai E {0,1} 을 구할 수 있는가?
- (기술적으로, 이것은 부분합(subset sum) 문제이다)
- 예
- 중량 집합 (62,93,26,52,166,48,91,141)
- 문제: 중량의 합 S=302 가 되는 중량 부분합을 구하여라
- 답: 62+26+166+48=302
- 일반적인(general) 배낭은 NP-complete이다
- 일반적인 배낭(GK: General knapsack)은 풀기 어려운 문제
- 하지만 빠르게 증가하는 배낭(SIK: superincreasing knapsack)은 풀기 쉬운 문제
- 각 중량은 그 중량보다 작은 모든 중량값의 합보다 크다
- 예: (2,3,7,14,30,57,120,251)
- S = a0W0+a1W1 +…+ an-1Wn-1를 만족하는 ai E {0,1} 을 구할 수 있는가?
배낭 암호화 시스템
- SIK 생성
- SIK를 GK로 변환
- 공개키: GK
- 비밀키: SIK + 변환 요소(conversion factors)
- 문제
- 공개키(GK)로는 암호화가 쉽다
- 비밀키(SIK)로는 복호화가 쉽다
- 비밀키 없이, GK를 풀어야 한다
- 시계 연산(“Clock” Arithmetic)
- 정수 x와 n에 대해, x mod n 은 x / n 의 나머지이다
- 예
- 7 mod 6 = 1
- 33 mod 5 = 3
- 33 mod 6 = 3
- 51 mod 17 = 0
- 17 mod 6 = 5
- 모듈러 덧셈(Modular Addition)
- 규칙
- 7 mod 6 = 1
- 7 = 13 = 1 mod 6
- ((a mod n) + (b mod n)) mod n = (a + b) mod n
- ((a mod n)(b mod n)) mod n = ab mod n
- 예
- 3 + 5 = 2 mod 6
- 2 + 4 = 0 mod 6
- 3 + 3 = 0 mod 6
- (7 + 12) mod 6 = 19 mod 6 = 1 mod 6
- (7 + 12) mod 6 = (1 + 0) mod 6 = 1 mod 6
- 규칙
- 모듈러 곱셈(Modular Multiplication)
- 3 x 4 = 0 (mod 6)
- 2 x 4 = 2 (mod 6)
- 5 x 5 = 1 (mod 6)
- (7 x 4) mod 6 = 28 mod 6 = 4 mod 6
- (7 x 4) mod 6 = (1 x 4) mod 6 = 4 mod 6
- 모듈러 역(Modular Inverses)
- x mod n의 덧셈의 역원은 -x이고, x가 0이 된다
- -2 mod 6 = 4 (왜냐하면 (2 + 4) mod 6 = 0 mod 6이기 때문)
- x mod n의 곱셈의 역원은 x-1이고, x가 1이 된다
- 3-1 mod 7 = 5 (왜냐하면 (3 x 5) mod 7 = 1 mod 7이기 때문)
- 2-1 mod 6은 존재하지 않는다
- 곱셈의 역원은 항상 존재하지는 않는다!
- x mod n의 덧셈의 역원은 -x이고, x가 0이 된다
- 서로소(Relative Primality)
- x와 y는 1을 제외한 공약수가 없으면 서로소
- x-1 mod y 는 x와 y가 서로소일 때만 존재한다
- x-1 mod y가 존재할 때 유클리드 알고리즘(Euclidean Algorithm)으로 쉽게 찾을 수 있다
- 암호화 과정
- SIK: (2,3,7,14,30,57,120,251)
- m = 41, n = 491 으로 잡는다
- m과 n은 서로소이면서, n은 SIK의 모든 원소의 합보다 크다
- GK:
- 2 x 41 mod 491 = 82
- 3 x 41 mod 491 = 123
- 7 x 41 mod 491 = 287
- 14 x 41 mod 491 = 83
- 30 x 41 mod 491 = 248
- 57 x 41 mod 491 = 373
- 120 x 41 mod 491 = 10
- 251 x 41 mod 491 = 471
- (82,123,287,83,248,373,10,471)
- 비밀키: m−1 mod n = 41−1 mod 491 = 12
- 공개키: (82,123,287,83,248,373,10,471), n=491
- 예: 10010110:
- 암호화
- 공개키 중 4개 선택: 82 + 83 + 373 + 10 = 548
- 복호화
- (548 x 12) mod 491 = 193 mod 491
- 쉬운 배낭 S를 통해 SIK를 푼다 => 193
- SIK: (2,3,7,14,30,57,120,251)
- 2 + 14 + 57 + 120 = 193, 해당하는 원소만 1로 표시하면
- 10010110
- 획득한 평문: 10010110
- 암호화
- 취약점
- 트랩도어(Trapdoor) 존재
- 모듈러 연산을 통해 SIK를 GK로 변환
- One-way
- GK는 암호화하기 쉽지만, 풀기 어렵다
- SIK는 풀기 쉽다
- 1983년 Apple II 컴퓨터에 의해 해독되었다.
- lattice reduction attack
- GK는 충분히 일반적이지 않으므로(special) 풀기 쉽다
- 트랩도어(Trapdoor) 존재
RSA
- Cocks (GCHQ)에 의해 고안됨
- Independently, by Rivest, Shamir and Adleman (MIT)
- 암호화
- p와 q가 충분히 큰 소수라고 하자
- N = pq 가 modulus가 된다
- (p−1)(q−1)과 소인수인 e를 선택한다
- ed = 1 mod (p−1)(q−1)이 성립하는 d를 찾는다
- 어떻게?
- 공개키: (N,e)
- 비밀키: d
- 암호화 과정
- 메세지 M을 암호화
- C = Me mod N
- 암호문 C를 복호화
- M = Cd mod N
- 공격자가 값(modulus) N을 인수분해(factor) 할 수 있다면, ed = 1 mod (p−1)(q−1) 이므로 e를 이용해 d를 쉽게 찾을 수 있다
- RSA가 해독된다
- 하지만 매우 어렵다
- 인수분해(factoring)가 RSA를 해독하는 유일한 수단인지는 알려지지 않았다
- 메세지 M을 암호화
- 증명
- C = Me mod N 이라고 하자
- M = Cd mod N = Med mod N
- 율러의 정리(Euler’s Theorem) 사용
- 만약 x가 n과 소인수이면 x@(n) = 1 mod n
- ed = 1 mod (p − 1)(q − 1)
- mod의 정의에 의해, ed = k(p − 1)(q − 1) + 1
- @(N) = (p − 1)(q − 1)
- 그러면 ed − 1 = k(p − 1)(q − 1) = k@(N)
- Med = M(ed−1)+1 = M x Med−1 = M x Mk@(N) = M x (M@(N))k mod N = M x 1k mod N = M mod N
- C = Me mod N 이라고 하자
- 토션트 함수(Totient Function)
- @(n)은 n보다 작은 n과 소인수인 양의 정수
- p가 소수일 때 @(p) = p-1
- p와 q가 소수일 때 @(pq) = (p-1)(q-1)
- @(n)은 n보다 작은 n과 소인수인 양의 정수
- Simple RSA 예제
- 큰 소수 두 개를 잡는다 (p = 11, q = 3)
- N = pq = 33
- (p−1)(q−1) = 20
- (p-1)(q-1)과 소인수인 수를 잡는다(e = 3)
- ed = 1 mod (p-1)(q-1)을 만족하는 d를 찾는다(d = 7)
- 현재 키
- 공개키: (N, e) = (33, 3)
- 비밀키: d = 7
- 메세지 M = 8
- C = Me mod N = 83 mod 33 = 512 mod 33 = 17 mod 33
- M = Cd mod N = 177 mod 33 = 410,338,673 mod 33 = 12,434,505 x 33 + 8 mod 33 = 8 mod 33
- 큰 소수 두 개를 잡는다 (p = 11, q = 3)
- 더 효과적인 RSA(More Efficient RSA)
- 모듈러 지수 예제(Modular exponentiation example)
- 520 = 95367431640625 = 25 mod 35
- 더 좋은 방법: 반복되는 squaring
- 20 = 10100 base 2
- (1, 10, 101, 1010, 10100) = (1, 2, 5, 10, 20)
- 2 = 1 x 2, 5 = 2 x 2 + 1, 10 = 2 x 5, 20 = 2 x 10
- 51 = 5 mod 35
- 52 = (51)2 = 52 = 25 mod 35
- 55 = (52)2 x 51 = 252 x 5 = 3125 = 10 mod 35
- 510 = (55)2 = 102 = 100 = 30 mod 35
- 520 = (510)2 = 302 = 900 = 25 mod 35
- 계산이 크지 않고 효율적이다
- 모듈러 지수 예제(Modular exponentiation example)
- 모든 유저에 대해 e = 3 이라고 가정하자 (하지만 같지 않은 N 이나 d)
- 공개키 계산은 2번의 곱셈만 필요하다
- 비밀키 계산은 여전히 비싸다
- 만약 M < N1/3이면 C = Me = M3 이므로, cube root attack이 가능하다
- For any M, if C1, C2, C3 sent to 3 users, cube root attack works
- 중국 나머지 정리(Chinese Remainder Theorem) 사용
- 메세지를 무작위 비트로 패딩하여 공격 방지 가능
- e = 216 + 1 also used
- 이산 로그(Discrete Logarithm)
- 디프-헬만(Diffie-Hellman)의 키 교환과 DSA에 기반을 둔다
- 율러의 정리(Euler’s Theorem)
- 모든 소인수 a와 n에 대하여 a@(n) = 1 (mod n)
- 만약 a와 n이 소인수라면, 위 식을 만족하는 정수가 최소 한 개 존재한다
- 최소 양의 정수 m이란?
- a (mod n)의 순서
- a에 의해 생성된 period의 길이
- n의 primitive root (또는 generator)
- m = @(n)
- 소수 p에 대해, a가 p의 primitive root이면 a, a2, …, ap-1 (mod p) 는 뚜렷하다
- 19의 primitive root: 2, 3, 10, 13, 14, 15
- Ordinary logarithm
- y = xi <-> logx(y)=i
- logx(1)=0, logx(x)=1
- logx(yz)=logx(y)+logx(z)
- logx(yr)=r * logx(y)
- Discrete logarithm
- a가 소수 p의 primitive root라고 하자
- a, a2, …, ap-1 (mod p) 는 1에서 (p-1) 의 값을 한 번씩 가진다
- 어떠한 정수 b에 대해 , 우리는 고유 지수(unique exponent)를 찾을 수 있다
- b = ai(mod p) where 0 <= i <= p-1
- i : discrete logarithm of b for the base a (mod p)
- dloga,p(b) = i
- 소수를 구하는 것 만큼이나 어렵다
디프 헬만(Diffie-Hellman)
- Williamson (GCHQ)이 고안
- Independently, by Diffie and Hellman (Stanford)
- 키 교환 알고리즘
- 공유된 대칭 키를 만들 때 사용된다
- 암호화나 서명에 쓰이지 않는다
- 보안성이 Discrete logarithm 문제의 풀기 어려움에 의존한다
- given g, p, and gk mod p find k
- p가 소수, g가 generator라 가정하자
- 모든 x E {1,2,…,p-1}에 대해 n s.t. x = gn mod p 가 존재한다
- A가 무작위 보안 값 a E {1, …, p-1}를 선택한다
- 보낼 때 ga mod p
- (ga)b mod p = gab mod p
- B가 무작위 보안 값 b E {1, …, p-1}를 선택한다
- 보낼 때 gb mod p
- (gb)a mod p = gab mod p
- K = gab mod p 를 대칭 키로 사용 가능하다
- 공격
- 공격자는 다음 정보를 볼 수 있다
- ga mod p
- gb mod p
- ga gb mod p = ga+b mod p != gab mod p 이므로 공격자가 discrete log 문제를 풀 수 있다면 a나 b를 찾을 수 있고, a나 b를 찾을 수 있다면 암호가 해독되지만 매우 어렵다
- 공격자는 다음 정보를 볼 수 있다
- 취약점
- man-in-the-middle (MITM)공격에 취약하다
- 공격자가 A와 B 모르게 gat mod p 를 A와 공유하고, gbt를 B와 공유한다
- MiM 공격 방지
- 디프-헬만 키 교환을 대칭키로 암호화한다
- 디프-헬만 키 교환을 공개키로 암호화한다
- 디프-헬만 값을 개인키로 서명한다
- 특정한 방법의 인증(authentication)이 필요하다
타원 곡선 암호(ECC: Elliptic Curve Crypto)
- 암호화 시스템이 아니라 공개 키 시스템의 수학적 연산의 다른 방법이다
- 디프-헬만(DH), RSA의 타원 곡선 암호 버전은 더 효율적일 수 있다
- 동일 수준의 보안에 더 적은 비트가 필요하지만, 연산은 더 복잡하다
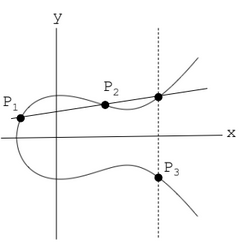
- 타원 곡선 E: y2 = x3 + ax + b
- 점 P1과 P2가 E 위에 있으면 P3 = P1 + P2를 정의할 수 있다
- 타원 곡선 암호화(Cryptography)
- 타원 곡선을 사용
- 변수(variables)와 계수(coefficients)는 유한한 필드의 요소(element)이다
- 2 families
- Prime curve over Zp
- Binary curve over GP(2m)
- Elliptic curve over Zp
- t2 mod p = (x3 + ax + b) mod p
디프 헬만 vs 타원 곡선 디프 헬만(DH vs. ECDH)
ECC Security
공개 키 표기법(Notation)
- A의 개인 키로 메세지 M을 서명: [M]A
- A의 공개 키로 메세지 M을 암호화: {M}A
- {[M]Alice}Alice = M
- [{M}Alice]Alice = M
공개 키 암호화의 사용
- 대칭키로 할 수 있는 모든 것이 가능하다
- 기밀성(Confidentiality)
- 공개 키로 암호화한다
- 무결성(Integrity)
- 개인 키로 서명한다
- 전자 서명(Digital signature)
- 무결성(Integrity)
- 부인 봉쇄(Non-repudiation)
- 해놓고 안했다고 발뺌하는 것 방지
- 대칭키에는 없는 기능
부인 봉쇄(Non-repudiation)
- A가 B로부터 물건 구매
- A가 주문에 A의 개인 키로 서명
- 물건이 갑자기 할인됨, A는 주문을 하지 않았다고 한다
- 하지만 물건의 주문은 A의 개인 키로만 알 수 있기 때문에 부인이 되지 않는다
- 하지만 누군가 키를 훔쳤다면 revocation 문제 발생
- 기밀성과 부인 방지 보장
- A가 B에게 메세지를 보낸다, 두 가지 방법
- A의 개인키로 서명하고 B의 공개키로 암호화한다 {[M]A}B
- A -> {[M]A}B -> B -> {[M]A}C -> C
- B의 공개키로 암호화하고 A의 개인키로 서명한다 [{M}B]A
- A -> [{M}Bob]Alice -> B -> [{M}Bob]Charlie -> C
- A의 개인키로 서명하고 B의 공개키로 암호화한다 {[M]A}B
- A가 B에게 메세지를 보낸다, 두 가지 방법
대칭키 vs 공개키
- 대칭키
- 빠르다
- PKI(public key infrastructure)가 필요 없다
- 공개키
- 서명(Signatures) 부인 방지(non-repudiation)
- 공유된 비밀이 없다
현실 기밀성(Real World Confidentiality)
- 하이브리드 암호화 시스템
- 키 생성을 위해 공개키 암호화 사용
- 데이터 암호화를 위해 대칭키 암호화 사용
- 단계
- A -> {K}B -> B
- B -> E(B’s data, K) -> A
- A -> E(A’s data, K) -> B
- B가 A에게 대화하는 것을 보장할 수 있는가?
- 공개키 인증서(Public Key Certificate)
- 비밀 키를 공유하지 않는다
- 어떻게 A의 공개키를 획득하고 검증할 수 있는가?
- 인증서 사용
- 디지털 인증서(Digital certificate)
- 인증한 사람의 이름, 공개키, (그 외 정보) 포함
- 인증서를 보증하는 (VeriSign)과 같은 issuer에 의해 서명된다
- 서명자의 공개 키에 의해 검증된다
인증 기관 (CA: Certificate Authority)
- 인증서에 서명하는 신뢰된 서드 파티(3rd party (TTP))
- 서명을 검증한다
- 해당 공용/개인 키 쌍 소유자의 ID 확인
- 인증서 원본의 ID를 확인하지 않는다
- 인증서는 공개적이다
- CA가 실수하면 안 된다
- CA가 Microsoft 인증서를 다른 사람에게 발급했었다
- 인증서의 기본 포맷은 X.509
공개 키 기반 시설(PKI: Public Key Infrastructure)
- 공개키 암호화를 안전하게 사용하기 위해 필요한 모든 부분으로 구성되었다
- 키 생성 및 관리
- 인증 기관
- 인증서 해지(Certificate revocation (CRLs)) 등
- 일반적 표준이 없다
PKI 신뢰 모델
- 독점 모델(Monopoly model)
- 하나의 보편적으로 신뢰된 기관이 CA
- VeriSign에 의해 선호된다
- CA가 손상되거나, 믿지 못할 경우 큰 문제 발생
- 과두제(Oligarchy)
- 여러 신뢰된 CAs
- 현대의 브라우저에서 쓰이는 방식
- 브라우저는 서명을 검증하기 위해 80개 이상의 인증서를 가지고 있다
- 유저가 어떤 CA를 신뢰할지 선택 가능
- 무정부 모델(Anarchy model)
- 모두가 CA
- 유저는 어떤 CA를 신뢰해야 할지 선택해야 한다
- PGP (Web of trust)에서 사용되는 방식
해쉬 함수(Hash functions)
해쉬 함수 동기(Motivation)
- A가 M으로 서명한다고 가정하자
- A는 M과 S(S = [M]Alice) 를 B에게 보낸다
- B는 M(M = {S}Alice)을 검증한다
- S만 보내도 되는가?
- M이 크다면 [M]Alice는 연산 비용이 많이 소모된다
- A가 h(M)이 M보다 훨씬 작을 때, h(M)으로 서명한다고 가정하자
- A는 M과 S = [h(M)]Alice를 B에게 보낸다
- B는 h(M) = {S}Alice을 검증한다
암호 해시 함수(Crypto Hash Function)
- 암호 해쉬 함수 h(x)가 존재해야 한다
- Compression
- 출력 길이가 작아야 한다
- Efficiency
- 모든 x에 대해 h(x)는 컴퓨터가 연산하기 쉬워야 한다
- One-way
- 주어진 y에 대해 h(x) = y를 만족하는 x를 찾는 것이 불가능해야 한다
- Weak collision resistance
- 주어진 x와 h(x)에 대해 h(y) = h(x)를 만족하는 y != x 인 조합을 찾는 것이 불가능해야 한다
- Strong collision resistance
- h(x) = h(y)를 만족하는 x != y를, x와 y에 대해 찾을 수 없어야 한다
- 충돌은 많지만 찾기 힘들다.
- Compression
생일 문제(Birthday Problem)
- pre 생일 문제
- 한 방에 N명이 있다
- N은 얼마나 커야 하는가?
- 한 방에 나와 같은 생일인 누군가가 있을 확률은 1/2(50%) 이상이다
- Solve: 1/2 = 1 − (364/365)N for N
- N = 253
- 생일 문제
- 한 방에 몇 명이 있어야 하는가?
- 한 방에 같은 생일인 누군가가 있을 확률은 1/2(50%) 이상이다
- 1 − 365/365 x 364/365 x … x (365−N+1)/365
- 위 식의 결과가 1/2이 되도록 하면 N = 23
- 모든 x와 y의 쌍(pair)을 비교하므로 최소 루트 365 이상이어야 한다
- 한 방에 몇 명이 있어야 하는가?
- 해쉬와 생일 문제
- 만약 h(x)가 N 비트이면, 2N개의 서로 다른 해쉬 값이 가능하다
- 루트(2N) = 2N/2
- 그러므로 2N/2개의 값을 해쉬하면 충돌(collision)이 발생될 것이다
- 안전한 N 비트 대칭(symmetric) 키의 break은 2N−1번의 시도를 요구한다
- 안전한 N 비트 해쉬의 break은 2N/2번의 시도를 요구한다
비암호화 해쉬(Non-crypto Hash)
- 1번 해쉬
- 데이터 X = (X0,X1,X2,…,Xn-1), 각 Xi는 바이트
- 해쉬 h(X) = X0+X1+X2+…+Xn-1
- Example: X = (10101010,00001111)
- Hash h(X) is 10111001
- 충돌하는 해쉬는 (00001111,10101010)로, 쉽게 찾을 수 있고 안전하지 않다
- 2번 해쉬
- 데이터 X = (X0,X1,X2,…,Xn-1)
- 해쉬 h(X) = nX0+(n-1)X1+(n-2)X2+…+ 1 x Xn-1
- (00000001,00001111)의 해쉬는 (00000000,00010001)와 같다
- one-way가 아니다
- 이 해시는 비암호화(non-crypto) 애플리케이션 rsync에 사용된다.
- 순환 중복 체크(CRC: Cyclic Redundancy Check)
- 우발적인(accidental) 데이터 변경 탐지
- 네트워크와 저장 장치에 사용된다
- 본질적으로, CRC는 장기 분할 문제(long division problem)의 나머지 부분이다
- 변속기 노이즈(transmission noise)로 인한 버스트 오류(burst errors)를 감지하는 데 적합하다
- 쉽게 충돌한다
- CRC가 암호화 애플리케이션(WEP)에 잘못 사용되는 경우가 있다
- CRC는 의도적인 조작을 감지하도록 설계되지 않았다
암호화 해쉬(Crypto Hashes)
- 해쉬는 블록의 메세지를 해슁함으로써 작동한다
- MD5
- Rivest가 고안
- 128 비트 해쉬
- 충돌이 발견되었다
- SHA
- SHA-0
- MD4 기반
- 취약점이 발견되었다
- SHA-1
- 미국 정부 표준
- 160 비트 해쉬, 블록 길이 512비트, Word 길이 32비트, 스텝 80
- 해독되지 않았지만 안전하지 않다
- SHA-2
- 2002년에 SHA-1의 개량 버전
- 224 비트 해쉬, 블록 길이 512비트, Word 길이 32비트, 스텝 64
- SHA-256
- 256 비트 해쉬, 블록 길이 512비트, Word 길이 32비트, 스텝 64
- SHA-512
- 512 비트 해쉬, 블록 길이 1024비트, Word 길이 64비트, 스텝 80
- 해쉬 과정
- 메세지를 블록으로(각 1024비트) 나눈다, 이 때 패딩(padding)과 메세지의 길이(L, 128비트 고정)을 메세지 뒤에 붙여서 1024비트를 만들어준다
- 512 비트 IV = H0을 만든다
- 첫 번째 블록과 H0을 해쉬 함수 F에 돌려 T0를 얻는다
- H0과 T를 + 연산하여 H1을 만든다
- 두 번째 블록과 H1을 해쉬 함수 F에 돌려 T1을 얻는다
- 반복…
- 해쉬 함수 F
- F는 미리 정해진 스텝(Steps)만큼 라운드를 진행한다
- 예제
- 메세지: 아스키 글자로 abc
- 패딩 이후: 61 62 63 80 00 00 00 00 + 00 00 00 00 00 00 00 00 x 18 + 00 00 00 00 00 00 00 18
- 18(hex) = 24(dec) = 8 bit x 3 = abc
- Initial values(H0)
- a: 6a09e667f3bcc908
- b: bb67ae8584caa73b
- c: 3c56ef372fe94f82b
- …
- h = 5be0cd19137e2179
- 80 라운드 진행
- 73a54f399fa4b1b2 10d9c4c4295599f6 d67806db8b148677 654ef9abec389ca9 …
- 해쉬 값
- H1,0 = a(6a09e667f3bcc908) + T0(73a54f399fa4b1b2) = ddaf35a193617aba
- …
- H1,7 = …
- 해쉬 결과
- H1,0 H1,1 H1,2 … H1,7
- SHA-3
- 차세대 NIST 해쉬 함수, 2012년 발표되었다
- 스펀지 구조(sponge construction) 기반 암호
- SHA-0
- 암호화 해쉬 디자인(Crypto Hash Design)
- 요구되는 속성: 눈사태 효과(avalanche effect)
- 1 비트의 메세지 변경이 최소 절반 이상의 암호문에 영향을 끼쳐야 한다
- 암호화 해쉬는 라운드(round)를 가진다
- 보안과 속도를 동시에 원한다
- 몇 라운드를 지나면 눈사태 효과가 나면서, 간단해야 한다
- 블록 암호 설계와 유사하다
- 요구되는 속성: 눈사태 효과(avalanche effect)
- 타이거 해쉬(Tiger Hash)
- 빠르고 강력하다
- Ross Anderson과 Eli Biham이 고안
- 설계 기준
- 안전
- 64비트 프로세서에 최적화
- MD5와 SHA-1을 쉽게 대체
- MD5/SHA-1와 동일하게 패딩된 512비트 블록 길이
- MD5/SHA-1와 다르게, 출력은 192비트(64비트 x 3)
- 중간(Intermediate) 라운드는 모두 192비트
- 4개의 S-box는 각각 8 bit가 64 비트를 맵핑한다
- 키 스케쥴(Key schedule)이 사용되었다
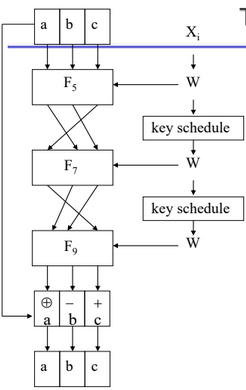
- 해쉬 과정
- 메세지 X
- X = (X0,X1,…,Xn-1)
- X는 패딩된다
- 각 Xi는 512 비트
- n번 반복
- 각 입력 블록 당 한번
- 초기 값
- a = 0x123456789ABCDEF
- b = 0xFEDCBA987654321
- c = 0xE096A5B4C3B2E187
- Final (a, b, c) 가 해쉬이다
- 메세지 X
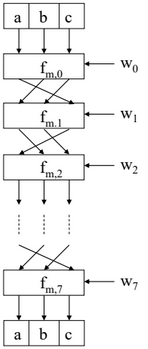
- 라운드 과정
- 각 Fm은 8 라운드(Fm,0에서 Fm,7)로 구성된다
- 512 비트 Wn를 Fm,n에 넣는다
- W=(w0,w1,…,w7)
- W는 입력 블록 Xi 중 하나이다
- 모든 라인은 64비트
- fm,i는 S-boxes에 의존(depend on)한다
- HMAC
- 해쉬된 맥(HMAC)으로 맥(MAC)을 계산할 수 있다
- 키 해쉬(keyed hash)의 예이다
- HMAC 연산의 두 가지 방법: h(K,M), h(M,K)
- HMAC을 h(K,M) 으로 계산해야 되는가?
- 해쉬는 블럭 안에서 계산된다
- 어떤 F와 상수(constant) A에 대해 h(B1,B2) = F(F(A,B1),B2)이면 h(B1,B2) = F(h(B1),B2)
- M`= (M,X)이라고 가정하자
- h(K,M’) = F(h(K,M),X)
- 공격자는 K 없이 M`의 HMAC을 공격할 수 있다
- h(M,K)이 더 나은가?
- 더 낫지만 만약 h(M’) = h(M) 일 경우 우리는 다음을 얻게 된다
- h(M,K)=F(h(M),K)=F(h(M’),K)=h(M’,K)
- 더 낫지만 만약 h(M’) = h(M) 일 경우 우리는 다음을 얻게 된다
- 올바른 HMAC
- RFC 2104에 기술되었다
- B를 해쉬 블록의 길이(byte)라고 가정하자
- B = 64 (MD5, SHA-1, Tiger)
- ipad = 0x36 B번 반복
- opad = 0x5C B번 반복
- HMAC(M,K) = H(K xor opad, H(K xor ipad, M))
- 해쉬 사용
- 인증(Authentication (HMAC))
- 메세지 무결성(Message integrity (HMAC))
- 메세지 지문(Message fingerprint)
- 데이터 손상 감지(Data corruption detection)
- 전자 서명 효율성(Digital signature efficiency)
- 대칭키로 할 수 있는 모든 것
- 온라인 경매(Auction)
- A, B, C가 참여자이고, A는 a, B는 b, C는 c의 금액을 입찰한다고 가정하자
- 입찰이 비밀로 유지되어야 한다
- A, B, C는 다음 해쉬를 보낸다 h(a), h(b), h(c)
- 모든 해쉬는 서버로 보내져 온라인에 포스트된다
- 입찰 a, b, c가 해쉬된 상태로 온라인에 보여진다
- 해쉬는 입찰가를 드러내지 않는다 (one way)
- 입찰가를 제시한 후 변경할 수 없다 (collision-resistant)
Other topics
비밀 공유(Secret Sharing)
- 비밀 S에 대해, 두 사람이 있어야 비밀을 풀 수 있다고 가정하자
샤미르의 비밀 공유(Shamir’s Secret Sharing)
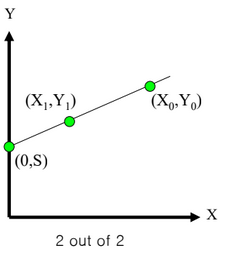
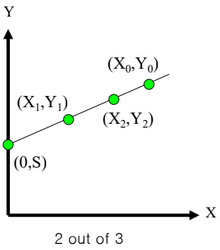
- 두 점이 직선을 결정한다
- (X0,Y0) 을 A에게, (X1,Y1) 을 B에게 준다
- 둘은 정보를 통해 협력(cooperate)하여 비밀 S를 찾을 수 있다
- n보다 같거나 작은 m에 대하여 “m out of n” 스키마(sheme)를 쉽게 만들 수 있다
- (X0,Y0) 을 A에게, (X1,Y1) 을 B에게, (X2,Y2) 을 C에게 준다
- A와 B, B와 C, C와 A는 정보를 통해 비밀 S를 찾을 수 있다
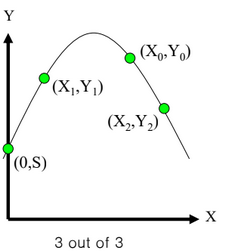
- (X0,Y0) 을 A에게, (X1,Y1) 을 B에게, (X2,Y2) 을 C에게 준다
- 세 점은 포물선(parabola)을 결정한다
- A, B, C는 협력(cooperate)을 통해 비밀 S를 찾을 수 있다
비밀 공유 예제(Secret Sharing Example)
- 키 에스크로(Key escrow)
- 당신의 키는 어딘가에 저장되어야 한다
- 키는 법원 명령(court order)과 함께 사용할 수 있다. 하지만 당신은 FBI가 열쇠를 보관하는 것을 믿지 않는다. 이 때 비밀 공유를 사용한다.
- 3개의 다른 정부 기관(government agencies)이 있고, 두 기관이 협력(cooperate)해야 키를 복구할 수 있다고 가정하자
- 위의 2 out of 3 scheme 사용
무작위 숫자(Random Numbers)
- 키 생성에 사용된다
- 대칭 키(Symmetric keys)
- RSA: 소수(Prime numbers)
- 디프 헬만(Diffie Hellman): 비밀 값(secret values)
- 특정 상황에서만 쓰기 위해 만든 무작위 숫자
- 때때로 순차적임이 허용되지만, 때때로 무작위여야 한다
- 그 외
- 시뮬레이션, 통계 등: 통계적으로만 무작위이면 된다
- 암호화 무작위 숫자는 통계적으로 무작위여야 하며 예측할 수 없어야 한다
- 텍사스 홀덤(Texas Hold’em Poker)
- 덱을 섞는 데 무작위 숫자가 사용되었지만, 무작위로 섞지 않아 실시간으로 예측이 가능하다
- 카드 섞기(Card Shuffle)
- 52! > 2~225 개의 가능한 셔플(shuffles)이 있다.
- 포커 프로그램이 셔플을 결정하는 데 ‘무작위 32비트 정수형’’ 을 사용했다 (232개의 셔플이 존재)
- Pascal pseudo-random number generator (PRNG): Randomize()를 사용했다
- PRNG의 seed 값이 자정 이후 밀리초 단위 기능이였다
- 하루는 227 밀리초 미만이므로 최대 227개의 셔플이 존재
- 서버와 시계를 동기화
- 테스트되어야 하는 셔플의 갯수 < 218
- 실시간으로 218 개의 셔플을 테스트할 수 있다
- 열린 카드를 통해 가능한 셔플을 테스트한다
- 공격자는 5 라운드 베팅 이후 모든 카드를 알게 된다
- 암호의 무작위 순서(Crypto random sequence)는 예측 불가능하다
- 예) RC4 cipher의 키 스트림(stream)
- 하지만 시드(seed) 선택에서 문제가 발생한다
- 초기 무작위 값을 어떻게 생성할까?
- 난수성(Randomness)
- 난수성의 척도는 엔트로피(Entropy)
- “진정한” 무작위성의 좋은 소스
- 방사성 붕괴(Radioactive decay)
- 양자 컴퓨터는 대중적이지 않다
- 하드웨어 장치(Hardware devices)
- 시장에 나와 있는 많은 좋은 것들
- 사람의 행동(Human behavior)
- 마우스 이동, 키보드 역학(dynamics) 등
- 소프트웨어
- 소프트웨어는 결정론적(deterministic)이다
- 외부의 ‘무작위’ 이벤트에 의존해야 한다
- 방사성 붕괴(Radioactive decay)
비밀에 대한 슈도 랜덤 프로세스 → 슈도 보안
pseudo random process for secret → pseudo-security
정보 은닉(Information Hiding)
- 디지털 워터마크(Digital Watermarks)
- 불법 재분배(illegal redistribution)를 확인하는 책임 식별 정보 숨기기
- 데이터에 ‘마크’를 추가하여 음악이나 소프트웨어 도용을 방지
- 종류
- Invisible ⎯ Not obvious the mark exists
- Visible ⎯ Such as TOP SECRET
- Robust ⎯ Readable even if attacked
- Fragile ⎯ Mark destroyed if attacked
- 디지털 음악에는 robust invisible 마크를 추가한다
- If pirated music appears on Internet, can trace it back to original source
- 오디오 파일에는 fragile invisible 마크를 추가한다
- If watermark is unreadable, recipient knows that audio has been tampered (integrity)
- 여러 타입의 조합은 가끔 사용된다
- visible + robust invisible
- 화폐에도 사용된다
- 1 평방 인치에는 전체 사진을 재구성할 수 있는 충분한 정보가 포함될 수 있다
- 사진이 손상된 경우 손상되지 않은 부분에서 워터마크를 읽을 수 있고 전체 사진을 재구성할 수 있다!
- 스테가노그래피(Steganography)
- 정보가 전송(transmitted)되고 있다는 사실 숨기기
- 비밀 통신 채널(covert channel)
- 헤로도토스(Herodotus) (그리스 440 BC)
- 노예의 머리를 깎아서 메세지를 쓰고 다시 자라게 함 -> 노예 전송, 머리 다시 깎음 (페르시아 침략 경고)
- 역사적으로 암호보다 많이 사용되었다
- 이미지와 스테가노그래피
- 이미지는 24비트 컬러(RGB: Red Green Blue) 사용
- While
- 0xAB 0x33 0xF0 is this color
- 0xAB 0x33 0xF1 is this color
- 자릿수가 낮은 비트는 색의 변화가 거의 없다
- 예
- 압축되지 않은 이미지 파일, BMP 포맷
- RGB의 낮은 비트에 우리가 원하는 데이터 삽입 가능
- 사람의 눈으로 식별 불가능하지만, 컴퓨터 프로그램은 가능하다
- 0xAB 0xCD 0xEF -> 0xA1 0xC2 0xE3
- html 문서
- <font color=”#000000” … /> -> <font color=”$010101”… />
- 압축되지 않은 이미지 파일, BMP 포맷
- 특정 포맷(jpg, gif, wav)은 사람이 구별하기 힘들다
- 문제점: 숨기기 쉽지만, 제거하기도 쉽다
- robust하기 위해서는 정보는 중요 비트에 저장되어야 한다
- 저장된 정보가 데이터를 손상시키면 안 된다
- 그러므로 robust는 까다롭다
- 정보 은닉이 의심되는 경우
- 공격자는 정보/워터마크를 읽을 수 없게 만들 수 있다.
- 공격자가 정보를 읽을 수 있을 수 있다 (Collusion attack)
- 원문(이미지, 오디오 등)을 고려, 워터마크 객체와 비교한다
Authentication
액세스 컨트롤(Access Control)
- 시스템 리소스 및 정보의 액세스 제어
- Authentication: 누구인지를 식별
- 접근 허용 여부 결정
- 기계와 인간 간의 인증
- 지식 인자(Knowledge factors) : 알고 있는 것
- 비밀번호, PIN, Social security number, 엄마의 maiden name, 생년월일, 애완동물 이름
- 소유 인자(Ownership factors) : 가지고 있는 것
- 스마트카드
- 상속 인자(Inherence factors) : 나 자신
- 지문
- 지식 인자(Knowledge factors) : 알고 있는 것
- 기계와 기계 간의 인증
- Authorization: 허용되었는지를 식별
- 액세스를 가지고 하는 행동 제약
- Authentication: 누구인지를 식별
당신이 아는 것(Something you know) - 비밀번호
- 비밀번호의 문제점
- 비밀번호는 오늘날 보안 엔지니어가 직면하고 있는 가장 큰 현실적인 문제 중 하나라고 말했다.
- 인간은 고품질 암호키를 안전하게 저장할 수 없고, 암호화 연산을 할 때 수용할 수 없는 속도와 정확성을 가지고 있다.
- 비밀번호 무분별한 재사용
- 비밀번호가 다른 방법보다 많이 쓰이는 이유
- 비용이 없다
- 편리하다
| 키 | 비밀번호 |
|---|---|
| 무작위 64 비트 길이(264개) | 무작위가 아닌 8 글자, 256가지의 문자 중 하나 = 2568 = (264 개) |
| 평균 약 263번 공격을 해야된다 | 263번보다 훨씩 적은 공격으로 비밀번호 획득이 가능하다 (사전 공격) |
- 비밀번호 실험
- 유저가 규칙을 잘 따라주지 않는다.
- Assigned 비밀번호는 때때로 가장 좋다
- 비밀번호가 assigned 되지 않았을 경우
- 패스프레이즈(passphrase) 기반으로 비밀번호 선택
- 비밀번호 크랙 툴을 사용해 취약성 테스트
- 주기적인 변경 필요
- 공격자가 가능한 것
- 특정 계정, 시스템의 모든 계정, 모든 시스템의 모든 계정을 타게팅
- Dos 공격
- 주 공격 경로
- 외부인 -> 일반 유저 -> 관리자
- 하나의 취약한 비밀번호만이 필요할 지도 모른다
- 비밀번호 재시도
- 비밀번호가 틀릴 경우 얼마나 잠겨 있어야 하는지
- What are +’s and -’s of each?
- 5초 잠김
- 자동 공격에 취약
- 5분 잠김
- Dos 공격에 취약
- SA가 서비스를 재시작 할 때까지
- 유저가 불편함
- 5초 잠김
- 비밀번호 파일: 해쉬화 된 비밀번호 저장(y = h(password))
- /etc/password
- root : x : 0 : 0 : root : /root : /bin/bash
- /etc/shadow
- vivek : $1$fnfffc$pGteyHdicpGOfffXX4ow#5 : 13064 : 0 : 99999 : 7 : : :
- /etc/password
- 사전 공격: 사전 단어를 해쉬화해서 공격한다
- 공격 방지: salt 값 사용 (y = h(password, s))
- salt값 s는 비밀번호 파일에 저장된다 (안전하지 않음)
- 공격자가 salt 값을 추가해야 하기 때문에 더 많은 연산이 소모된다.
- 공격 방지: salt 값 사용 (y = h(password, s))
- 로그인 비밀번호 vs ATM PIN
- 사회공학(Social Engineering)적 공격
- 버그, 키로거(keystroke logging), 스파이웨어
- 패스워드 크랙 툴
- Password Crackers
- Password Portal
- L0phtCrack and LC4 (Windows)
- http://www.l0phtcrack.com/
- http://www.youtube.com/watch?v=g2Yr4QprDok
- John the Ripper (Unix)
- Good article on password cracking
- Passwords - Conerstone of Computer Security
- http://www.symantec.com/connect/ko/articles/password-crackers-ensuring-security-your-password
당신인 것(Something you are) - 생체 정보(Biometrics)
- “You are your key” ⎯ Schneier
- 지문, 안면, 음성, 걸음걸이 인식
- 특징
- 싸고, 믿을만하다.
- 아직 그 약속에 부응하지 못함 - Has not lived up to its promise (yet)
- 이상적인 생체측정학
- Universal ⎯ 거의 모두에게 적용되어야 한다
- 실제로, 모두에게 적용되는 것은 없다
- Distinguishing ⎯ 확실하게 구분되어야 한다
- 100% 보장 불가능
- Permanent ⎯ 측정된 물리적인 특성이 변하지 않아야 한다
- 오랜 기간 동안 유효해야 한다
- Collectable ⎯ 데이터 수집이 쉬워야 한다
- 고객이 협조적인가에 따라 달려 있다
- 안전하고, 사용이 쉬워야 한다
- Universal ⎯ 거의 모두에게 적용되어야 한다
- 지문 인식(Fingerprint Biometric)
- Loop(double)
- Whorl
- Arch
- 손 인식(Hand Geometry)
- 손의 모양을 측정한다
- 손과 손가락의 너비
- 손가락들의 길이
- 장점
- 빠르다(1분 등록, 5초 인식)
- 손 대칭(Hands symmetric): 다른 손을 뒤로 사용 가능
- 단점
- 어리거나 늙으면 적용 불과
- 높은 에러율
- 손의 모양을 측정한다
- 홍채 인식(Iris Patterns)
- 홍채는 쌍둥이 포함 모두 다르다
- 일생동안 똑같다
- 공격 방법
- 정교하게 찍은 눈 사진
- 공격 방어 방법
- 빛을 이용하여 ‘살아있는’ 홍채인지 판별
- 생체 정보는 만들기 어렵지만 공격이 가능하다
- 지문 복사
- 소프트웨어나 데이터베이스, 신뢰된 경로 전복시키기(subvert)
- 고장난(broken) 생체 인식을 어떻게 취소(revoke)하는가?
- Biometrics are not foolproof!
- Biometric use is limited today
- That should change in the future…
당신이 가지고 있는 것(Something you have)
- 자동차 키, 노트북, 맥 주소, 비밀번호 생성기, ATM 카드, 스마트카드
- Password Generator
- Alice says to Bob “I’m Alice”
- Alice gets “challenge” R from Bob
- Alice has pwd generator and knows PINs
- Alice enters PIN, R into password generator
- Alice retrives F(R) from password generator
- Alice sends “response”(=F(R)) back to Bob
2-factor Authentication
- 위 요인(Something you know, Something you have, Something you are) 중 2개를 사용한다
- bearer가 보안 시스템에 액세스하는 것이 허용됨의 보장을 늘리기(increase the assurance) 위해
- 예시
- ATM: Card, PIN
- 신용카드: 카드, 시그니처(signature)
- 비밀번호 생성기: 장치, PIN
- 스마트카드 + 비밀번호/PIN
SSO: Single Sign-on
- 비밀번호를 반복적으로 입력하는 번거로움
- “자격 증명(Credentials)”이 어디에서나 사용자와 함께 있다
- 후속 인증(Subsequent authentication)은 사용자에게 투명함(transparent)
- 예시
- Microsoft: Passport
- Everybody else: Liberty Alliance
- Based on Security Assertion Markup Language (SAML)
OAuth and OpenID
- OAuth
- 액세스 위임(access delegation)을 위한 개방형 표준
- 웹 사이트나 앱이 비밀번호를 주지 않고 다른 웹사이트에서 자신의 정보에 접근할 수 있도록 허용한다.
Web Cookies
- 쿠키는 웹 사이트에서 제공하고 사용자의 컴퓨터에 저장됨
- 쿠키는 웹사이트에서 데이터베이스를 인덱스한다
- 웹은 상태가 없는 프로토콜(HTTP)을 쓰므로 쿠키는 세션 전체에 걸쳐 상태를 유지한다
- 쿠키는 또한 세션 내에서 상태를 유지한다
- 매우 약한 형태의 인증이지만 single sign-on처럼 동작할 수 있다